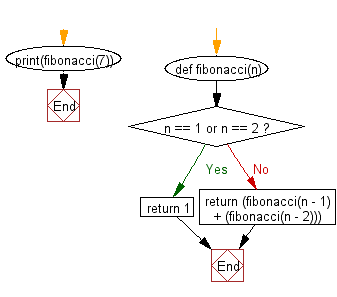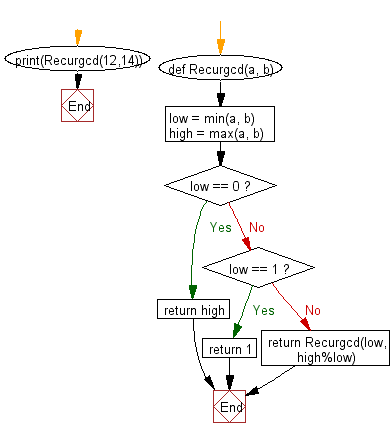
Recurgcd(12,14)=return Recurgcd(low, high%low)
Recurgcd(12,14)=return Recurgcd(12,2))
Recurgcd(12,14)=return Recurgcd(return Recurgcd(2,0))
Recurgcd(12,14)=return Recurgcd(return 2)
Recurgcd(12,14)=return 2
Monday, June 29, 2020
Write a Recursive Python program to find the greatest common divisor (gcd) of two integers.
def Recurgcd(a, b):
low = min(a, b)
high = max(a, b)
if low == 0:
return high
elif low == 1:
return 1
else:
return Recurgcd(low, high%low)
print(Recurgcd(12,14))
Write a Python Recursive program to calculate the value of 'a' to the power 'b'.
def power(a,b):
if b==0:
return 1
elif a==0:
return 0
elif b==1:
return a
else:
return a*power(a,b-1)
print(power(3,4))
power(3,4)=3*power(3,3)
power(3,4)=3*3*power(3,2)
power(3,4)=3*3*3*power(3,1)
power(3,4)=3*3*3*3
power(3,4)=81
Write a Python program to calculate the harmonic sum of n-1.
Note: The harmonic sum is the sum of reciprocals of the positive integers. Example: harmonic series
def harmonic_sum(n):
if n < 2:
return 1
else:
return 1 / n + (harmonic_sum(n - 1))
print(harmonic_sum(7))
print(harmonic_sum(4))
Explanation:
harmonic_sum(7)=1/7+harmonic_sum(6)
harmonic_sum(7)=1/7+1/6+harmonic_sum(5)
harmonic_sum(7)=1/7+1/6+1/5+harmonic_sum(4)
harmonic_sum(7)=1/7+1/6+1/5+1/4+harmonic_sum(3)
harmonic_sum(7)=1/7+1/6+1/5+1/3+harmonic_sum(2)
harmonic_sum(7)=1/7+1/6+1/5+1/3+1/2+harmonic_sum(1)
harmonic_sum(7)=1/7+1/6+1/5+1/3+1/2+1
Write a Python program to calculate the sum of the positive integers of n+(n-2)+(n-4)... (until n-x =< 0).
def sum_series(n):
if n < 1:
return 0
else:
return n + sum_series(n - 2)
print(sum_series(6))
print(sum_series(10))
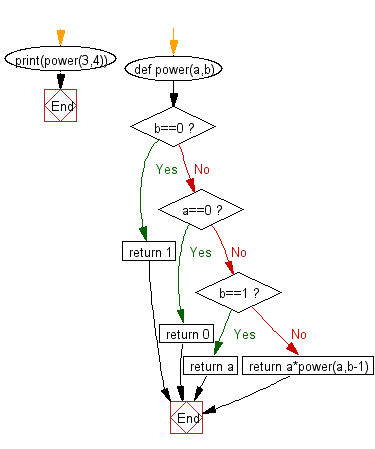
Sample Output:
12 30
sum_series(6)=6 + sum_series(4)
sum_series(6)=6 + 4+sum_series(2)
sum_series(6)=6 + 4+sum_series(2)
sum_series(6)=6 + 4+2+0
Python Recursive Function for Fibonacci Sequence
def fibo(n):
if n == 1 or n == 2:
return 1
else:
return (fibo(n - 1) + (fibo(n - 2)))
print(fibo(7))
Explanation:
fibo(7)=fibo(6)+fibo(5)
fibo(7)=(fibo(5)+fibo(4))+(fibo(4)+fibo(3))
fibo(7)=(fibo(4)+fibo(3)+fibo(3)+fibo(2)+fibo(3)+fibo(2)+fibo(2)+fibo(1))
fib(7)=fibo(3)+fibo(2)+fibo(2)+fib(1)+fibo(2)+fib(1)+1+fibo(2)+fib(1)+1+1+1
fib(7)=fibo(2)+fib(1)+1+1+1+1+1+1+1+1+3
fib(7)=1+1+8+3
fib(7)=13
Python Recursive Program for Digit Addition of Integer's
def sumDigits(n):
if n == 0:
return 0
else:
return n % 10 + sumDigits(int(n / 10))
print(sumDigits(345))
print(sumDigits(45))
pyhton Recursive Program for Fcatorial Calculation
def factorial(n):
if n <= 1:
return 1
else:
return n * (factorial(n - 1))
print(factorial(5))
Subscribe to:
Posts (Atom)